2024 CrewCTF Write-ups

8.4下午打的，没看几个题，不过感觉挺有意思的😈

• Crypto - Boring LCG

附件：

• boring-lcg.zip

import os
from sage.all import *
set_random_seed(1337)
Fp = GF(6143872265871328074704442651454311068421530353607832481181)
a, b = Fp.random_element(), Fp.random_element()

flag = (os.getenv('flag') or 'crew{submit_this_if_desperate}').encode()
s = Fp.from_integer(int.from_bytes(flag[len('crew{'):-len('}')], 'big'))

out = []
for _ in range(12): out.extend(s:=a*s+b)
print([x>>57 for x in out])
# [50, 32, 83, 12, 49, 34, 81, 101, 46, 108, 106, 57, 105, 115, 102, 51, 67, 34, 124, 15, 125, 117, 51, 124, 38, 10, 30, 76, 125, 27, 89, 14, 50, 93, 88, 56]

题目本身非常短，但是推柿子🍅有点麻烦。这个过程相当于将明文\(\text{Flag🚩}\in\mathbb{F}_{p^3}\)上做了如下操作：

\[ c_{i+1}=\text{LCG}(c_i)=a\cdot c_i+b\in\mathbb{F}_{p^3},\qquad c_0=\text{Flag🚩}\in\mathbb{F}_{p^3} \]

各种参数都是由某个已知的随机数种子生成的，因此我们知道所有的参数：

modulus = x^3 + 6741171702277637523*x^2 + 11441156621098138177*x + 18315300953692143458
a = 11096584571873777345*z3^2 + 10557248725682989278*z3 + 3979752675954023529
b = 10472345338873147245*z3^2 + 15508141526608210223*z3 + 15735705331444753146
p = 18315300953692143461

此外，

\[ \begin{aligned} \text{LCG}(c_{i0}+c_{i1}\alpha+c_{i2}\alpha^2)&=k_{i0}+k_{i1}\alpha+k_{i2}\alpha^2\\ &=c_{(i+1)0}+c_{(i+1)1}\alpha+c_{(i+1)2}\alpha^2\\ &\in\mathbb{F}_{p^3} \end{aligned} \]

其中，

\[ \left\{\begin{aligned} k_{i2}&=&a_2c_{i2}(m_2^2-m_1)-(a_2c_{i1}+a_1c_{i2})m_2+b_2\\ & &+(a_2c_{i0}+a_1c_{i1}+a_0c_{i2})\\ k_{i1}&=&a_2c_{i2}(m_1m_2-m_0)-(a_2c_{i1}+a_1c_{i2})m_1+b_1\\ & &+(a_0c_{i1}+a_1c_{i0})\\ k_{i0}&=&a_2c_{i2}m_0m_2-(a_2c_{i1}+a_1c_{i2})m_0+b_0\\ & &+a_0c_{i0}\\ \end{aligned}\right. \]

\(\alpha\)是\(\mathbb{F}_{p^3}\)的本原生成元，而\(m_0,m_1,m_2\)表示\(\mathbb{F}_{p^3}\)的本原多项式的分量。

题目给了\(c_{ij}\)高8比特位的数据，也即

\[ c_{ij}=\tilde{c}_{ij}\cdot 2^{57}+x_{ij},\qquad i=1,\cdots,12,\ j=0,1,2 \]

我们可以构造如下的格：

\[ \newcommand{\bs}{\boldsymbol} \bs L=\begin{pmatrix} \beta\cdot\bs A_{(n+1)\times(n-3)} & \bs B_{n+1}\\ \beta\cdot p\bs I_{n-3} & \bs O\\ \end{pmatrix}_{(2n-2)\times(2n-2)} \]

其中\(n=36\)，

\[ \bs B = \begin{pmatrix} 1 & & & & \\ & 1 & & & \\ & & \ddots & & \\ & & & 1 & \\ & & & & \gamma \\ \end{pmatrix}_{n+1} \]

\(\beta,\gamma\)均为较大的数，\(\bs A\)中的各项见本节结尾的代码。于是，\(\bs L\)中含有如下的格点：

\[ \begin{pmatrix}x_{10} & x_{11} & x_{12} & x_{20} & \cdots & x_{12,2} & 1 &\Bigg\vert & k_1 & \cdots & k_{n-3}\end{pmatrix}\cdot \bs A=\begin{pmatrix}\smash[b]{\underbrace{0\quad \cdots\quad 0}_{n-3}} & x_{10} & x_{11} & x_{12} & x_{20} & \cdots & x_{12,2} & \gamma \end{pmatrix} \]

\(x_{ij}\)的大小大致为\(2^{57}\)，据此我们可以通过求解\(\bs L\)上的CVP问题来找到待求的\(x_{ij}\)，求出所有的\(x_{ij}\)以后，对\(c_1=(\tilde{c}_{10}+\tilde{c}_{11}\alpha+\tilde{c}_{12}\alpha^2)\cdot 2^{57}+(x_{10}+x_{11}\alpha+x_{12}\alpha^2)\)在\(\mathbb{F}_{p^3}\)上进行\(\text{LCG}\)的逆变换即可得到明文：

\[ \text{Flag🚩}=c_0=\text{LCG}^{-1}(c_1)=\frac{c_1-b}{a}\in\mathbb{F}_{p^3} \]

#sage

def kannan_cvp(mat, target, reduction=(lambda x: x.LLL()), weight=None):
    if weight is None:
        weight = max(target)
    L = block_matrix([[mat, 0], [-matrix(target), weight]])
    for row in reduction(L):
        if row[-1] < 0:
            row = -row
        if row[-1] == weight:
            return row[:-1] + target

set_random_seed(1337)
Fp = GF(6143872265871328074704442651454311068421530353607832481181)
a, b = Fp.random_element(), Fp.random_element()
p = 18315300953692143461
z3 = Fp.gen()

m0, m1, m2, _ = Fp.modulus()
a0, a1, a2 = a
b0, b1, b2 = b

c = [50, 32, 83, 12, 49, 34, 81, 101, 46, 108, 106, 57, 105, 115, 102, 51, 67, 34, 124, 15, 125, 117, 51, 124, 38, 10, 30, 76, 125, 27, 89, 14, 50, 93, 88, 56]
n = len(c)
A = matrix(ZZ, n + 1, n - 3)
shift = 57
for i in range(n//3 - 1):
    ci0 = c[i*3 + 0] << shift
    ci1 = c[i*3 + 1] << shift
    ci2 = c[i*3 + 2] << shift
    ci0_ = c[i*3 + 3] << shift
    ci1_ = c[i*3 + 4] << shift
    ci2_ = c[i*3 + 5] << shift
    row = i*3
    col = i*3 + 0
    A[row + 0, col] = a0
    A[row + 1, col] = -a2*m0
    A[row + 2, col] = -a1*m0 + a2*m0*m2
    A[row + 3, col] = -1
    A[-1, col] = a0*ci0 + b0 - (a2*ci1 + a1*ci2)*m0 + a2*ci2*m0*m2 - ci0_
    col = i*3 + 1
    A[row + 0, col] = a1
    A[row + 1, col] = a0 - a2*m1
    A[row + 2, col] = -a1*m1 + a2*(m1*m2-m0)
    A[row + 4, col] = -1
    A[-1, col] = a0*ci1 + a1*ci0 + b1 - (a2*ci1 + a1*ci2)*m1 + a2*ci2*(m1*m2-m0) - ci1_
    col = i*3 + 2
    A[row + 0, col] = a2
    A[row + 1, col] = a1 - a2*m2
    A[row + 2, col] = a0 - a1*m2 + a2*(m2**2-m1)
    A[row + 5, col] = -1
    A[-1, col] = (a2*ci0 + a1*ci1 + a0*ci2) + b2 - (a2*ci1 + a1*ci2)*m2 + a2*ci2*(m2**2-m1) - ci2_

A1 = block_matrix([[A, 1],[p, 0]])

beta = 2**100
gamma = 2**100
A1[A.dimensions()[0] - 1, -1] *= gamma
A1[:, :n-3] *= beta

A_ = A1.LLL()

f = lambda x: round(2**(x-1)+(2**x-2**(x-1))/2)
center = [0]*A.dimensions()[1] + [f(57) for i in range(A.dimensions()[0]-1)] + [beta]

v = kannan_cvp(A1, vector(center))
print(v)

Flag🚩：

crew{n0rm4l_LCG_but_1_d1d_xxx}

Proof of Concept：

• sol_boring-lcg.sage

• Crypto - Admin

附件：

• admin.zip

关键的部分在这里：

cipher = AES.new(key, AES.MODE_GCM, nonce=iv)
curusername = b'not_admin_username_' + str(i).encode()
enc, tag = cipher.encrypt_and_digest(pad(curusername, blksize))
return (curusername.decode(), iv.hex(), enc.hex(), tag.hex())

这是一种名为Galois/Counter Mode (GCM)的分组密码操作模式，如图所示：

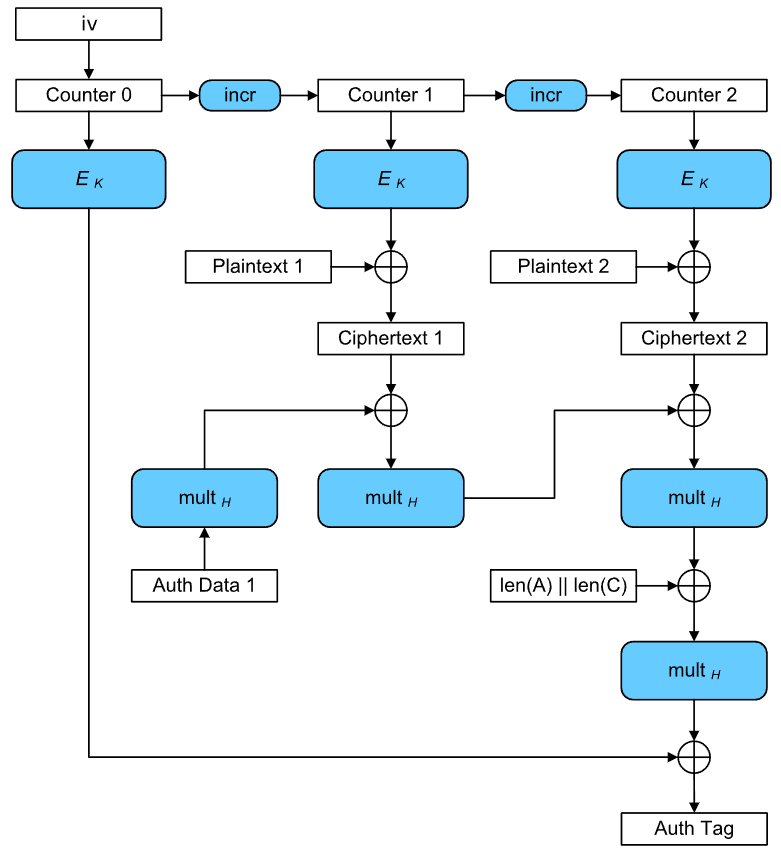
更详细的解释参见NIST给的文档：

而cipher.encrypt_and_digest是一种认证加密的操作（authenticated encryption），返回的数据包含密文（ciphertext）以及认证标签（authenticated tag），在知道key与iv时可以使用cipher.decrypt_and_verify来验证密文-标签对是否有效，若有效则该函数返回解密后的数据，否则抛出错误。一次认证加密的流程如下：

Encoding:

 b127  ||  b126  ||  ...  ||  b001  ||  b000    (MSB)
  ^         ^         ^        ^         ^
  |         |         |        |         |
  v         v         v        v         v
α^000  +  α^001  +   ...  +  α^126  +  α^127    (LSB)

对于每128比特位为一组的数据，我们将其转换为\(\mathbb{F}_{2^{128}}=\mathbb{F}_2[\alpha]/(\alpha^{128}+\alpha^7+\alpha^2+\alpha+1)\)上的元素，并且从左往右的每个比特位按照次数\(i\)从小到大的顺序放在\(\alpha^i\)的系数中（如上所示），以此来进行后续的计算，生成标签\(T\)的核心流程相当于：

• \( H=\text{AES}_K(0^{128}) \)


• \( J_0=F_K(\text{IV}) \)


• \( J=\text{AES}_K(J_0) \)


• \( \text{GHASH}_H(X)=H\cdot X\in\mathbb{F}_{2^{128}}\qquad \text{with }X\text{ 128 bits} \)


• \( \text{GHASH}_H(X_1\Vert \cdots\Vert X_{n-1} \Vert X_n)=H\cdot X_n+H\cdot \text{GHASH}_H(X_1\Vert\cdots \Vert X_{n-1})\in\mathbb{F}_{2^{128}}\qquad \text{with }X_i\text{ 128 bits} \)


• \( L=[\text{len}(A)]_{64}\Vert[\text{len}(C)]_{64} \)


• \( S=\text{GHASH}_H(\underbrace{A\Vert 0^v}_{\text{128 bits}} \Vert \underbrace{C\Vert 0^u}_{128\cdot K\text{ bits}} \Vert L) \)


• \( \begin{aligned}T&=\text{GCTR}_K(J_0,S)\\&=J+S\in\mathbb{F}_{2^{128}}\end{aligned} \)

其中\(\text{GCTR}\)函数的图示如下：

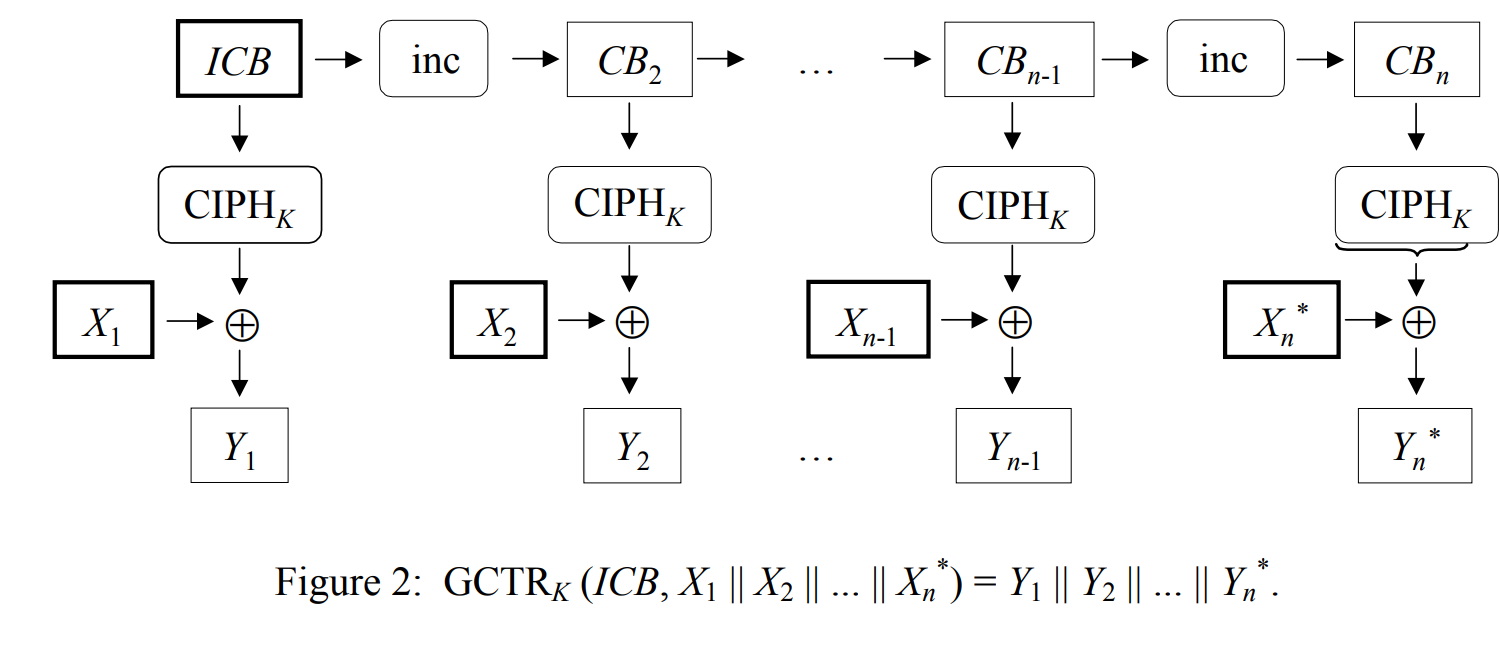
而\(J_0=F_K(\text{IV})\)是仅与初始化向量\(\text{IV}\)和密钥\(K\)有关的函数，在本题中我们可以使用相同的IV，比如

\[ \text{IV}=\underbrace{0000\cdots00}_{128} \]

来保证认证加密以及认证解密过程中\(J_0\)与\(J\)是不变的。我们申请两个密文-标签对：

\[ (C_1,T_1),\ (C_2,T_2) \] \[ \begin{aligned} C_1&=C_{11}\Vert C_{12}\\ C_2&=C_{21}\Vert C_{22}\\ \end{aligned} \]

我们知道，在密文的生成过程

\[C=\text{GCTR}_K(\text{inc}_{32}(J_0),P)\]

这一步中，明文\(P\)的第一个块\(P_{11}\)每次都会与\(\text{AES}_K(\text{inc}_{32}(J_0))\)异或，据此，在知道这个明文块\(P_{11}\)与对应密文块\(C_{11}\)的情况下，我们可以控制第一个块中密文的内容（事实上后续的块也类似地可以）。我们可以构造一个对应明文为admin\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b\x0b的密文块\(C_3\)。

接下来，我们尝试伪造\(C_3\)的标签\(T_3\)。将\(T_1,T_2\)展开：

\[ \begin{aligned} T_1 &= (((A\cdot H + C_{11})\cdot H + C_{12})\cdot H + L_1)\cdot H + J\\ T_2 &= (((A\cdot H + C_{22})\cdot H + C_{22})\cdot H + L_2)\cdot H + J\\ \end{aligned} \]

也即

\[ \begin{aligned} T_1 &= A\cdot H^4 + C_{11}\cdot H^3 + C_{12}\cdot H^2 + L_1\cdot H + J\\ T_2 &= A\cdot H^4 + C_{21}\cdot H^3 + C_{22}\cdot H^2 + L_1\cdot H + J\\ \end{aligned} \tag{1}\label{1} \]

在本题中，对于\(C_1,C_2,C_3\)而言，我们有

L1 = b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00'
L2 = b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00'
L3 = b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x80'

而对于附加数据\(A\)而言，均有

A = b'\x00\x00\x00\x00\x00\x00\x00\x00'

将\eqref{1}中两式相加：

\[ T_1+T_2 = (C_{11}+C_{21})\cdot H^3 + (C_{12}+C_{22})\cdot H^2 \]

因此，\(H\)是\(\mathbb{F}_{2^{128}}\)上如下方程的根：

\[ (C_{11}+C_{21})\cdot x^3 + (C_{12}+C_{22})\cdot x^2 + (T_1+T_2) = 0 \]

于是，

\[ J = T_1 + A\cdot H^4 + C_{11}\cdot H^3 + C_{12}\cdot H^2 + L_1\cdot H \]

因此我们可以伪造出\(T_3\)：

\[ T_3 = A\cdot H^3 + C_3\cdot H^2 + L_3\cdot H + J \]

将IV、\(C_3\)与\(T_3\)拼接在一起作为token发送即可获得admin身份。

\[ \text{token🔒} = \text{IV}\Vert C_3\Vert T_3 \]

上述攻击方法称为The Forbidden Attack。

# https://meowmeowxw.gitlab.io/ctf/utctf-2020-crypto/
# sage

from Crypto.Util.number import long_to_bytes as lb
from Crypto.Util.number import bytes_to_long as bl
from binascii import unhexlify, hexlify
from sage.all import *
import struct

def bytes_to_polynomial(block, a):
    poly = 0
    # pad to 128
    bin_block = bin(bl(block))[2 :].zfill(128)
    # reverse it to count correctly, wrong don't reverse it lol
    # bin_block = bin_block[::-1]
    for i in range(len(bin_block)):
        poly += a^i * int(bin_block[i])
    return poly

def polynomial_to_bytes(poly):
    return lb(int(bin(poly.integer_representation())[2:].zfill(128)[::-1], 2))

def convert_to_blocks(ciphertext):
    return [ciphertext[i:i + 16] for i in range(0 , len(ciphertext), 16)]

def xor(s1, s2):
    if(len(s1) == 1 and len(s1) == 1):
        return bytes([ord(s1) ^^ ord(s2)])
    else:
        return bytes(x ^^ y for x, y in zip(s1, s2))

F, a = GF(2^128, name="a", modulus=x^128 + x^7 + x^2 + x + 1).objgen()
R, x = PolynomialRing(F, name="x").objgen()

# Set correct values
C1 = convert_to_blocks(bytes.fromhex("ca6a3e623d125bdcddfe5c6e0ecba0911162c4f4469a62c32f1598ce9b161f92"))
T1 = bytes.fromhex("79be7f8880af8d18b8abac496fb690d2")
C2 = convert_to_blocks(bytes.fromhex("ca6a3e623d125bdcddfe5c6e0ecba0911162c4f5469a62c32f1598ce9b161f92"))
T2 = bytes.fromhex("abb63fd177e59f360ef2b3786e7fe4a9")
C3 = convert_to_blocks(bytes.fromhex("c5612754327d3dbeb8aa221660b2c5fb"))

L = struct.pack(">QQ", 0 * 8, len(C1) * 128)
C1_p = [bytes_to_polynomial(C1[i], a) for i in range(len(C1))]
C2_p = [bytes_to_polynomial(C2[i], a) for i in range(len(C2))]
C3_p = [bytes_to_polynomial(C3[i], a) for i in range(len(C3))]
T1_p = bytes_to_polynomial(T1, a)
T2_p = bytes_to_polynomial(T2, a)
L_p = bytes_to_polynomial(L, a)
L3 = struct.pack(">QQ", 0 * 8, len(C3) * 128)
L3_p = bytes_to_polynomial(L3, a)
# Here G_1 is already modified to include the tag
G_1 = (C1_p[0] * x^3) + (C1_p[1] * x^2) + (L_p * x) + T1_p
G_2 = (C2_p[0] * x^3) + (C2_p[1] * x^2) + (L_p * x) + T2_p
G_3 = (C3_p[0] * x^2) + (L3_p * x)
P = G_1 + G_2
auth_keys = [r for r, _ in P.roots()]
for H, _ in P.roots():
    EJ = G_1(H)
    T3 = G_3(H) + EJ
    print("H: " + str(H) + "\nT3: " + str(polynomial_to_bytes(T3).hex()))

Flag🚩：

crew{priviledge_escalation_admin_by_crypto_technique}

Proof of Concept：

• sol_admin.sage

• Reverse - HTML - 1

附件：

• html.zip

本题显然不是正经的HTML（HyperText Markup Language），事实上，根据html-lang.org的介绍：

这里的HTML指的是一种面向堆栈的编程语言，代码中的每一种标签都代表了一种栈操作（详见html-lang.org），我们的任务则是分析出这个程序的逻辑以找到判断密码是否正确的逻辑。首先程序在<main>中定义了几个函数：

• l(c)：相当于

  function l(c) {
      let e = document.createElement("p");
      let r = e;
      if (c) {
          r = c;
          e.appendChild(c);
          return r;
      }
      r = document.body.appendChild(e);
      return r;
  }
  

  所以应该没啥用。

• w(a, b)：相当于乘方 - pow(base, exp)
• x(a, b)：相当于异或 - xor(a, b)
• m(a, b)：相当于取模 - mod(n, m)
• r(z, o)：相当于特殊的RC4加密（解密？） - rc4(key, pt)
• y()：与button#j的onclick绑定了，验证密码是否正确的逻辑就在这个函数中。

Level 1中只需要知道这么多就够了，接下来遇到的一个问题是y()中验证部分的代码量略大，我们可以将翻译这部分代码的工作交给人工组来完成按照HTML编程语言的逻辑，编写一个以压栈与弹栈为基础的解释器来翻译这些代码，并将途中用到的操作以表达式的形式储存下来。完成了翻译的工作以后，由于表达式是涉及到加法、乘法与异或的等式方程组，因此交由Z3来完成即可。此外，可以使用BeautifulSoup提取出HTML代码中的标签，遍历这些标签并挨个解析为对应的栈操作即可。

html_doc =    # ...

from bs4 import BeautifulSoup
soup = BeautifulSoup(html_doc, 'html.parser')

queue = []
ops = []
stack = []

for child in soup.select("code > *"):
    if child.name == 'a':
        queue.extend(list(child.children))
    queue.append(child)

for child in queue:
    if child.name == 'data':
        ops.append('data %s' % child['value'])
    elif child.name == 'cite':
        assert child.text == 'p'
        ops.append('p')
    elif child.name == 'a':
        if child['href'] == 'javascript:x()':
            ops.append('xor')
        else:
            raise TypeError("Invalid function name: \"%s\"" % child['href'])
    elif child.name == 'address':
        ops.append('address')
    elif child.name == 'ul':
        ops.append('multiply')
    elif child.name == 'dd':
        ops.append('add')
    elif child.name == 'sub':
        ops.append('subtract')
    elif child.name == 'em':
        ops.append('equal')
    elif child.name == 'b':
        ops.append('and')
    else:
        raise TypeError("Invalid operation name: \"%s\"" % child.name)

ops = ops[::-1]
while ops:
    op = ops.pop()
    if op.startswith('data'):
        stack.append(int(op.split('data ')[1]))
    elif op == 'p':
        stack.append('p')
    elif op == 'xor':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            stack.append('(%s ^ %s)' % (b, a))
        else:
            stack.append(b ^ a)
    elif op == 'address':
        a = stack.pop()
        b = stack.pop()
        assert b == 'p'
        assert not 'p' in str(a)
        stack.append('p%s' % a)
    elif op == 'multiply':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            stack.append('(%s * %s)' % (b, a))
        else:
            stack.append(b * a)
    elif op == 'add':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            stack.append('(%s + %s)' % (b, a))
        else:
            stack.append(b + a)
    elif op == 'subtract':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            stack.append('(%s - %s)' % (b, a))
        else:
            stack.append(b - a)
    elif op == 'equal':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            stack.append('(%s == %s)' % (b, a))
        else:
            stack.append(int(b == a))
    elif op == 'and':
        a = stack.pop()
        b = stack.pop()
        if 'p' in str(a) or 'p' in str(b):
            #stack.append('(%s and %s)' % (b, a))
            stack.append('%s, %s' % (b, a))
        else:
            stack.append(int(bool(int(b) & int(a))))
    else:
        raise TypeError("Invalid operation name: \"%s\"" % child.name)

assert len(stack) == 1
expr = stack[0]
expr = f'[{expr}]'

from z3 import *

p0,p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15 = [BitVec(pp, 8) for pp in 'p0,p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15'.split(',')]
eqs = eval(expr)
s = Solver()
for eq in eqs:
    s.add(eq)
assert s.check() == sat
model = s.model()
print(bytes([int(str(model[pp])) for pp in [p0,p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15]]))

Password🔒：

pWnBHiIp6vfoK6Y8

Flag🚩：

crew{w3lc0m3_t0_h7m1_3nj0y_th3_n3xt_l3v3l_9c6c1af9}

Proof of Concept：

• sol_html1.py

• (After Match) Pwn - Format muscle

附件：

• format-muscle.zip

首先musl里的printf中用来表示偏移的$最多只能偏移九个QWORD，此外，偏移数必须全部在1 ~ n内，且1 ~ n内不允许有未出现的偏移数，其中n是某个正整数。因此我们只能通过不断地添加标识符来产生偏移。（参见musl-1.2.2/src/stdio/vfprintf.c，430~655）

在成功做到任意地址写之后，篡改exit的hook即可。

Proof of Concept：

• exp_format-muscle.py

• (Not Solved) Reverse - HTML - 2

附件与HTML - 1是一样的，本题也是附件中所说的level 2，相比起level 1来新增了更多的函数以及变量，感觉做法应该是差不多的，懒得看了😴💤。

• (Not Solved) Crypto - Bigger and better

附件：

• bigger-and-better.zip

多项式的系数非常地庞大，再者，各种生成随机数的函数都有个前缀secrets，让人很难不联想到这可能是一个与PRNG有关的问题，没详细研究了😴💤。

• (Not Solved) Crypto - Noisy Encryption

附件：

• noisy-encryption.zip

这个肯定是PRNG的问题，但是没有详细研究😴💤。