27~28号打的,就看了两个题。

- roots
附件:
关键部分是这里
sum(a * Decimal(p).sqrt() for a, p in zip(otp(data), key))Decimal的精度是2024个十进制位的有效数字,我们可以将输出中的小数都乘以10的某个幂次——比如\(10^{2004}\)——来让其变成整数,从而将问题转化为整环上的方程组问题:
其中\(C_1,C_2,C_3,C_4\)是输出乘以\(10^{2004}\)以后得到的结果(整数),观察发现,\(X_1,X_2,X_3\)相当于我们加密用的key,并且相对于OTP过程中使用的key \(K_{ij}\)以及误差 \(\varepsilon_i\)来说都非常地巨大。
回忆ACD问题(Approximate Common Divisor Problem)的解法
\(L_1\)中的格点有短向量
\[ \vec{v}_1 = \begin{pmatrix}\vec{a}\cdot\vec{\varepsilon} & \vert & \vec{a}\end{pmatrix} \]其中
\[ \vec{a}\in\text{ker}(K)=K^{\perp}\subset\mathbb{Z}^4,\qquad \vec{\varepsilon}=\begin{pmatrix}\varepsilon_1 & \varepsilon_2 & \varepsilon_3 & \varepsilon_4\end{pmatrix} \]对\(L_1\)进行格基规约以后可以得到三个不同的\(\vec{a}\in\text{ker}(K)\)向量。
显然,三组OTP key \((K_{1i},K_{2i},K_{3i},K_{4i}),\ i=1,2,3\) 均在\((K^{\perp})^{\perp}\)中,我们需要另造一个格\(L_2\),用来从中筛选出我们需要的向量,而\(L_2\)刚好可以由我们从\(L_1\)中获得的三个\(\vec{a}\)向量组成。
\[ L_2=\begin{pmatrix} \vec{a}_1\\ \vec{a}_2\\ \vec{a}_3\\ \end{pmatrix} \]实际计算的过程中可以发现,\(L_2\)的最短向量中各项的比特位数在62左右,而我们的目标向量中各项的比特位数不超过64,这也就是说,\(L_2\)中数量级在在64比特位以内的格点不会太密集,这是一个好消息,因为我们可以通过解决\(L_2\)的最近向量问题来找到许多个符合比特位数要求的格点,然后三三计算各分量的异或,这个异或值可以作为判断这三个格点是否是OTP key的依据。
可以使用Kannan CVP算法来求解非方阵格基的CVP问题
#https://github.com/maple3142/lll_cvp
def kannan_cvp(mat, target, reduction=(lambda x: x.LLL()), weight=None):
if weight is None:
weight = max(target)
L = block_matrix([[mat, 0], [-matrix(target), weight]])
for row in reduction(L):
if row[-1] < 0:
row = -row
if row[-1] == weight:
return row[:-1] + target我们可以让目标向量遍历\((2^{n_1-1},2^{n_2-1},2^{n_3-1},2^{n_4-1})\)与\((2^{n_1},2^{n_2},2^{n_3},2^{n_4})\)之间的中心位置(\(n_i\in\{64,63,\cdots,59\}\)),将得到的所有不同的最近向量存储下来作为候选值,最后三三检测是否满足要求即可。
Flag🚩:
corctf{I'm_r00t1ng_f0R_U!!!!!!!}Proof of Concept:
- two-wrongs
附件:
オーマイガー、Quantum Circuit!(momoi音)

得研究量子线路,这里我只关注了一个量子逻辑门——CNOT(Controlled NOT)。CNOT本质上是对两个量子位的一个酉变换:
\[ \text{CNOT}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{pmatrix} \] \[ \text{CNOT}\left(a\left\vert 00\right\rangle+b\left\vert 01\right\rangle+c\left\vert 10\right\rangle+d\left\vert 11\right\rangle\right)=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ \end{pmatrix} \begin{pmatrix} a\\ b\\ c\\ d\\ \end{pmatrix}=\begin{pmatrix} a\\ b\\ d\\ c\\ \end{pmatrix}=a\left\vert 00\right\rangle+b\left\vert 01\right\rangle+d\left\vert 10\right\rangle+c\left\vert 11\right\rangle \]对于目标的两个量子位而言,它相当于一个受控的异或:
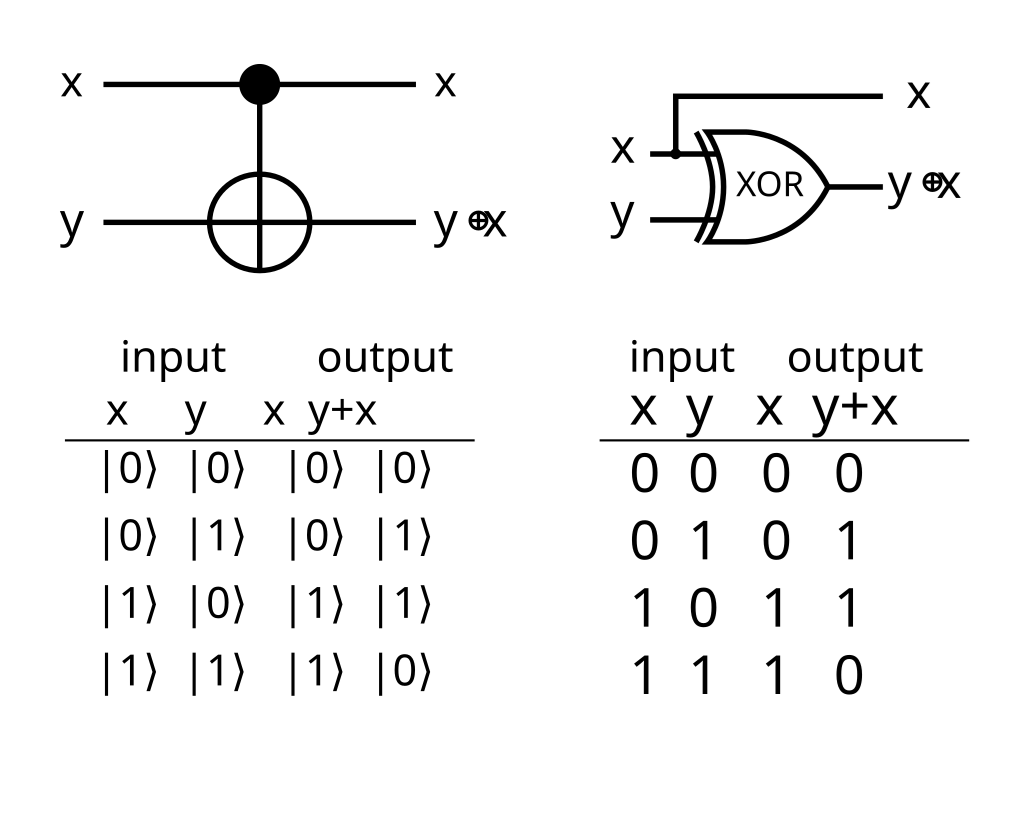
CNOT相当于一个受控的Pauli-X矩阵诱导的变换,其在Qiskit中的符号为cx,以上图为例,上述接线方法被记为cx(x,y)。此外,它还有两个兄弟——cy与cz。Pauli-X、Pauli-Y、Pauli-Z矩阵作为\(\text{SL}_2(\mathbb{C})/\{\pm 1\}\)上的元素阶均为2,可以猜到cy与cz也具有类似的功能。
让我们回到本题中来,只分析代码中含有cx的部分,可以看出,main寄存器中第6个Qubit携带了待解密比特的信息,它应当被接入到res寄存器中,此外,还应将Qubit 1、Qubit 2分别与res相接从而与Qubit 6再次异或,这样,在没有其他干扰的情况下我们的res携带了正确的比特信息。
接下来考虑线路中其他的干扰对Qubit 6的影响,我们可以将该系统剩余的部分视作一个黑盒子,始终按照上述方式接线并观察输出与sensor_val之间的关系,可以发现,当sensor_val的比特位组合为如下三种情况时,目标字节中对应位置处原本正确的比特位会被翻转,否则不翻转。
110 000 -> flip
010 000 -> flip
100 000 -> flip
others -> hold此外,前三比特与后三比特不同时不全为0,因此即便我们将每个sensor_val的后三比特位给mask掉,我们也能判断目标比特是否会被翻转,据此便可尝试与靶机交互。
Flag🚩:
corctf{c0rr3ct_CORr3Ct!nG_9aenq}Proof of Concept: