本文讨论组合数学中的几个经典问题:烷基计数问题、单烯烃计数问题与烷烃计数问题。即给定正整数\(n\),求含有\(n\)个碳原子的烷基、单烯烃与烷烃的同分异构体数(不考虑环与立体异构)。
- Burnside引理
Burnside引理(Burnside's lemma),有时被称作Not Burnside's lemma,其基本表述为
\[ \newcommand{\abs}[1]{\left\vert #1\right\vert} \newcommand{\lcm}[1]{\mathrm{lcm}\left(#1\right)} \newcommand{\gcd}[1]{\mathrm{gcd}\left(#1\right)} \newcommand{\d}{\mathrm{d}} \newcommand{\C}[2]{{#1 \choose #2}} \newcommand{\S}[2]{{#1 \brace #2}} \abs{X/G}=\frac{1}{\abs{G}}\sum\limits_{g\in G}\abs{X^g} \]其中
\[ X^g=\{x\in X:g\cdot x=x\} \]将\(\abs{G}\)乘到等式左边,则上式在直觉上显然成立。此外,由于
\[ \sum\limits_{g\in G}\abs{X^g}=\#\{(g,x)\in G\times X:g\cdot x=x\}=\sum\limits_{x\in X}\abs{G_x} \tag{1}\label{1} \]其中\(G_x=\{g\in G: g\cdot x=x\}\)是\(G\)的稳定子(stabilizer)。轨道-稳定子定理(orbit-stabilizer theorem)表明,
\[ \abs{G\cdot x}=[G:G_x]=\abs{G}/\abs{G_x} \]于是
\[ \sum\limits_{x\in X}\abs{G_x}=\sum\limits_{x\in X}\abs{G}/\abs{G\cdot x}=\abs{G}\sum\limits_{x\in X}\frac{1}{\abs{G\cdot x}}=\abs{G}\sum\limits_{A\in X/G}\sum\limits_{x\in A}\frac{1}{\abs{A}}=\abs{G}\cdot \abs{X/G} \]即
\[ \sum\limits_{g\in G}\abs{X^g} = \abs{G}\cdot \abs{X/G} \]\(\eqref{1}\)式表明,Burnside引理通过改变枚举量来使计数过程更加方便。
【例1】 考虑立方体上的上色问题,即给定一个三维立方体,每个面上可以涂三种不同的颜色,求本质不同(rotationally distinct)的上色方案数。
在Burnside引理中取\(X\)为\(3^6\)种上色方案的组合,\(G\)取立方体上的旋转变换群(\(\abs{G}=\abs{S_4}=4!=24\)),那么对于每类旋转变换,\(X\)中在该类变换下均保持不变的元素个数有如下对应关系:
- 一个单位旋转变换,可以拆成\((1)(2)(3)(4)(5)(6)\),对应\(3^6\)个\(X\)中元素
- 六个以面为轴的90°旋转变换,可以拆成\((1)(2)(3456)\),对应\(3^3\)个\(X\)中元素
- 三个以面为轴的180°旋转变换,可以拆成\((1)(2)(34)(56)\),对应\(3^4\)个\(X\)中元素
- 八个以相对顶点连线为轴的120°旋转变换,可以拆成\((123)(456)\),对应\(3^2\)个\(X\)中元素
- 六个以对边中点连线为轴的180°旋转变换,可以拆成\((12)(34)(56)\),对应\(3^3\)个\(X\)中元素
上述拆分中,变换的每个子轮换对应的若干个面必须具有相同的颜色才能使该子轮换保持这些面的颜色不变。所求方案数即为
\[ \abs{X/G}=\frac{1}{4!}(3^6+6\cdot 3^3+3\cdot 3^4+8\cdot 3^2+6\cdot 3^3)=57 \]- Pólya计数定理
Pólya计数定理(Pólya enumeration theorem),是Burnside引理的扩展。在例1的上色过程中,设\(X\)为立方体的六个面,\(G\)是上例中的旋转变换群(\(S_4\)),\(Y\)是所有颜色的集合。现在我们引入权重的概念,将每一种颜色——也即\(Y\)中的元素\(y\)——与一个非负整数\(w(y)\)(称作权重)对应,而最终整个立方体的上色方案对应的权重为所有面上颜色的权重之和,这样做的好处将在后续的几个例子中体现出来。
现在设权重\(w\)对应的颜色有\(f_w=\#\{y\in Y:w(y)=w\}\)种,那么\(f_w\)的生成函数为
\[ f(t)=f_0+f_1t+f_2t^2+\cdots \]定义cycle index:
\[ Z_G(t_1,t_2,\cdots,t_n)=\frac{1}{\abs{G}}\sum\limits_{g\in G}t_1^{c_1(g)}t_2^{c_2(g)}\cdots t_n^{c_n(g)} \]其中\(n=\abs{X}\)(在例1中\(n=6\),但是\(t_5\)与\(t_6\)并没有被用到),而\(c_k(g)\)是\(g\)的分解中长度为\(k\)的轮换个数。
考虑从\(X\)到\(Y\)的映射
\[ Y^X\ni\varphi:X\rightarrow Y \]例1中每个本质不同的上色方案\(\varphi\)均为\(Y^X/G\)中的元素,而其权重则是
\[ w(\varphi)=\sum\limits_{x\in X}w(\varphi(x)) \]在例1上述权重恒为0。利用Pólya计数定理可以很方便地统计对于特定的\(w\)满足\(w(\varphi)\)的\(\varphi\)的个数\(F_w=\#\{\varphi\in Y^X:w(\varphi)=w\}\)。Pólya计数定理的一般表述为
\[ F(t)=Z_G\left(f(t),f(t^2),\cdots,f(t^n)\right) \]其中\(F(t)\)是上述\(F_w\)的生成函数。
【例2】 设例1中的颜色种数为\(m\),那么
\[ Z_G(t_1,t_2,t_3,t_4)=\frac{1}{24}(t_1^6+6t_2^2t_4+3t_1^2t_2^2+8t_3^2+6t_2^3) \] \[ f(t)=m \] \[ \abs{Y^X/G}=F(0)=Z_C(m,m,m,m)=\frac{1}{24}(m^6+3m^4+12m^3+8m^2) \]【例3】 求含有\(n\)个点与\(m\)条边的不同构的简单无向图的个数。
考虑对完全图\(K_n\)涂上两种颜色黑与白,黑色代表有边,权重为\(1\),而白色代表没边,权重为\(0\),我们有
\[ f(t)=1+t \]对于\(G=S_n\)中的每一个元素,我们总是可以将其分拆成若干个轮换的积,设对于每种分拆\(\pi\),长度为\(k\)的轮换个数为\(\lambda_k(\pi)\),那么\(G\)中分拆符合\(\pi\)这种形式的元素个数为 \[ \begin{aligned} N_{\pi}&=\frac{n!\cdot \prod\limits_{k=1}^n (P_k!)^{\lambda_k(\pi)}}{\prod\limits_{k=1}^n\lambda_k(\pi)!\cdot (k!)^{\lambda_k(\pi)}}\\ &=\prod\limits_{k=1}^n\frac{n!}{\lambda_k(\pi)!\cdot k^{\lambda_k(\pi)}} \end{aligned} \]
其中,\(P_k=(k-1)!\)表示\(k\)个不同元素构成的圆排列数。从而我们考虑点集\(X_0\)在\(G\)下的cycle index
\[ \begin{aligned} Z_{G}(t_1,\cdots,t_n)&=\frac{1}{n!}\sum\limits_{\pi}N_{\pi}\prod\limits_{k=1}^nt_k^{\lambda_k(\pi)}\\ &=\sum\limits_{\pi}\prod\limits_{k=1}^n \frac{1}{\lambda_k(\pi)!}\left(\frac{t_k}{k}\right)^{\lambda_k(\pi)} \end{aligned} \tag{2}\label{2} \]我们知道,边集\(X\)在\(g\)的作用下的变化可以表示为\(g'\),并且\(g'\)的分拆方式可以很容易地由\(g\)的分拆方式确定,例如:
\[ \begin{aligned} g &= (123456)(789A)(BCD)\\ g' &=\color{red}{(\overline{12}\ \overline{23}\ \overline{34}\ \overline{45}\ \overline{56}\ \overline{61})(\overline{13}\ \overline{24}\ \overline{35}\ \overline{46}\ \overline{51}\ \overline{62})(\overline{14}\ \overline{25}\ \overline{36})}\\ &\qquad\color{green}{(\overline{78}\ \overline{89}\ \overline{9A}\ \overline{A7})(\overline{79}\ \overline{8A})}\\ &\qquad\color{blue}{(\overline{BC}\ \overline{CD}\ \overline{DB})}\\ &\qquad\color{yellow}{(\overline{17}\ \overline{28}\ \overline{39}\ \overline{4A}\ \overline{57}\ \overline{68}\ \overline{19}\ \overline{2A}\ \overline{37}\ \overline{48}\ \overline{59}\ \overline{6A})}\\ &\qquad\color{yellow}{(\overline{18}\ \overline{29}\ \overline{3A}\ \overline{47}\ \overline{58}\ \overline{69}\ \overline{1A}\ \overline{27}\ \overline{38}\ \overline{49}\ \overline{5A}\ \overline{67})}\\ &\qquad\color{magenta}{(\overline{1B}\ \overline{2C}\ \overline{3D}\ \overline{4B}\ \overline{5C}\ \overline{6D})}\\ &\qquad\color{magenta}{(\overline{1C}\ \overline{2D}\ \overline{3B}\ \overline{4C}\ \overline{5D}\ \overline{6B})}\\ &\qquad\color{magenta}{(\overline{1D}\ \overline{2B}\ \overline{3C}\ \overline{4D}\ \overline{5B}\ \overline{6C})}\\ &\qquad\color{cyan}{(\overline{7B}\ \overline{8C}\ \overline{9D}\ \overline{AB}\ \overline{7C}\ \overline{8D}\ \overline{9B}\ \overline{AC}\ \overline{7D}\ \overline{8B}\ \overline{9C}\ \overline{AD})}\\ \end{aligned} \]\(g\)对应的项是\(t_6t_4t_3\),而\(g'\)对应于\(t_{12}'^3 t_6'^5 t_4' t_3'^2 t_2'\),据此我们可以计算出\(X\)在\(G\)下的cycle index
\[ \begin{aligned} \widetilde{Z_{G}}(t_1,\cdots,t_n) &=\sum\limits_{\pi}\left(\prod\limits_{k=1}^n \frac{1}{\lambda_k(\pi)!\cdot k^{\lambda_k(\pi)}}\right)\cdot\underbrace{\Phi_n\left(t_1,\cdots,t_n\right)}_{\color{gray}{\text{Mysterious yet!}}} \end{aligned} \]最终
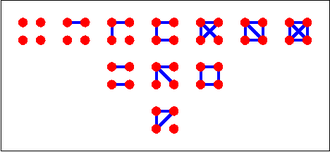
\[ \begin{aligned} F(t)&=\widetilde{Z_G}\left(f(t),\cdots,f(t^n)\right)\\ &=\sum\limits_{\pi}\left(\prod\limits_{k=1}^n \frac{1}{\lambda_k(\pi)!\cdot k^{\lambda_k(\pi)}}\right)\cdot\Phi_n\left(1+t,\cdots,(1+t)^n\right) \end{aligned} \]例如,当\(n=4\)时,我们有
\[ \begin{aligned} 4&=4\\ &=3+1\\ &=2+2\\ &=2+1+1\\ &=1+1+1+1 \end{aligned} \] \[ \begin{aligned} Z_G(t_1,\cdots,t_4)&=\sum\limits_{\pi}\prod\limits_{k=1}^4 \frac{1}{\lambda_k(\pi)!\cdot k^{\lambda_k(\pi)}}t_k^{\lambda_k(\pi)}\\ &=\frac{1}{1!\cdot 4^1}t_4^1+\frac{1}{1!\cdot 3^1\cdot 1!\cdot 1^1}t_3^1t_1^1+\frac{1}{2!\cdot 2^2}t_2^2\\ &\quad+\frac{1}{1!\cdot 2^1\cdot 2!\cdot 1^2}t_2^1t_1^2+\frac{1}{4!\cdot 1^4}t_1^4\\ &=\frac{1}{24}(t_1^4+6t_1^2t_2+3t_2^2+8t_1t_3+6t_4) \end{aligned} \] \[ \widetilde{Z_G}(t_1',\cdots,t_6')=\frac{1}{24}(t_1'^6+9t_1'^2t_2'^2+8t_3'^2+6t_2't_4') \] \[ \begin{aligned} F(t)&=\frac{1}{24}\left((1+t)^6+9(1+t)^2(1+t^2)^2+8(1+t^3)^2+6(1+t^2)(1+t^4)\right)\\ &=t^6+t^5+2t^4+3t^3+2t^2+t+1 \end{aligned} \]它对应下图
上述所有过程——包括\(\Phi_n(t_1,\cdots,t_n)\)的计算——均可以交由计算机高效地完成。
- 烷基计数
设烷基数的生成函数为\(A(x)\)。(不含环的)烷基可以看作一棵无向树,并且有且仅有一个碳原子是最为特殊的,将其选作树根,它至多有三个度,当度不足\(3\)时,缺少的边视作连接了零个碳原子(\(A(0)=1\))。令\(X\)为树根的三条边,\(Y\)为所有烷基,\(G\)取\(S_3\),即三条边的所有置换,根据\(\eqref{2}\)计算\(X\)在\(G\)下的cyclic index:
\[ Z_G(t_1,t_2,t_3)=\frac{1}{6}(t_1^3+3t_1t_2+2t_3) \]根据Pólya计数定理得到
\[ \begin{aligned} A(x) &= 1+x\cdot Z_G\left(A(x),A(x^2),A(x^3)\right)\\ &= 1+x\frac{A(x)^3+3F(x)A(x^2)+2A(x^3)}{6} \end{aligned} \tag{3}\label{3} \]此外,设烷基数为\(a_n\),利用Burnside引理计算
\[ \begin{aligned} a_{n+1} &= \frac{1}{6}(\underbrace{A_{n3}}_{\color{gray}{(1)(2)(3)}}+3\underbrace{A_{n2}}_{\substack{\color{gray}{ (12)(3)\\(13)(2)\\(23)(1)}}}+2\underbrace{A_{n1}}_{\substack{\color{gray}{(123)\\(132)}}}) \end{aligned} \]其中
\[ \begin{aligned} A_{n1} &= \sum_{\scriptstyle 3i=n \atop \scriptstyle i\in\mathbb{N}} a_i\\ A_{n2} &= \sum_{\scriptstyle 2i+j=n \atop \scriptstyle i,j\in\mathbb{N}} a_ia_j\\ A_{n3} &= \sum_{\scriptstyle i+j+k=n \atop \scriptstyle i,j,k\in\mathbb{N}} a_ia_ja_k\\ \end{aligned} \]同理也可以得到\(\eqref{3}\)式。
- 烯烃计数
设烯烃数的生成函数为\(F(x)\)。只有一个不饱和度的烯烃可以看作是一根特殊边(碳碳双键)的两端连上了两棵碳原子数至少为\(1\)的无向树(\(F(0)=0\))。令\(X\)为双键两端的两棵子树,\(Y\)为所有烷基,\(G\)取\(S_2\),即双键两端两棵树的所有置换,根据\(\eqref{2}\)计算\(X\)在\(G\)下的cyclic index:
\[ Z_G(t_1,t_2)=\frac{1}{2}(t_1^2+t_2) \]根据Pólya计数定理得到
\[ \begin{aligned} F(x) &= Z_G\left(A(x)-1,A(x^2)-1\right)\\ &= \frac{(A(x)-1)^2+A(x^2)-1}{2} \end{aligned} \tag{4}\label{4} \]此外,设烯烃数为\(f_n\),利用Burnside引理计算
\[ \begin{aligned} f_{n} &= \frac{1}{2}(\underbrace{F_{n2}}_{\color{gray}{(1)(2)}}+\underbrace{F_{n1}}_{\substack{\color{gray}{(12)}}}) \end{aligned} \]其中
\[ \begin{aligned} F_{n1} &= \sum_{\scriptstyle 2i=n \atop \scriptstyle i\in\mathbb{N_+}} a_i\\ F_{n2} &= \sum_{\scriptstyle i+j=n \atop \scriptstyle i,j\in\mathbb{N_+}} a_ia_j\\ \end{aligned} \]同理也可以得到\(\eqref{4}\)式。
- 烷烃计数
在烷基计数与烯烃计数中,树中都存在一个特殊的节点或者边,然而,对于一般的烷烃而言并不存在这样的节点或边。
众所周知,碳原子数相同时,在不考虑立体异构的情况下,不含环的烷烃不同当且仅当分子中的所有碳原子之间的邻接关系不变(up to isomorphism)。设树中点的等价类数为\(p\),边的等价类数为\(q\),现在尝试考虑\(p\)和\(q\)之间存在的关系。
- 假设树中存在一条对称边,即该边两端的子树完全相同(同构),那么显然\(p=q\)
- 假设树中不存在该对称边,那么从树中任选一个碳原子将其作为树的根,从树的叶子节点开始向根回溯,同一层的两个碳原子若等价,则其连接到上一层碳原子的边也等价;若这两个碳原子不等价,那么它们分属两个等价类,并且连接到上一层碳原子的边也分属两个等价类。不管是哪种情况,它们对\(p-q\)这个式子都没有贡献,因此最终只有树的根节点向\(p-q\)式中贡献\(1\),于是\(p=q+1\)
如果用\(s\in\{0,1\}\)来表示树中是否存在对称边,并且当且仅当存在对称边时\(s=1\),那么
\[ p-q+s=1 \tag{5}\label{5} \]显然,对于\(n\)个碳原子的烷烃\(s=1\)的情况数有\(a_{n/2}\)种,也即两端的两个烷基均含有\(\frac{n}{2}\)个碳原子,并且\(n\ge 2\)于是我们得到了\(s_n\)的生成函数
\[ S(x)=A(x^2)-1 \]依照图中点的等价关系的定义,从某两个等价类中分别任选一个碳原子(代表元)进行特殊标记,那么其周围的四个基团本质相同(up to \(S_4\))当且仅当这两个等价类是同一个等价类,因此含有\(n\)个碳原子的本质不同的烷烃中碳原子等价类数的总和\(p_n\)恰好满足如下的生成函数:
\[ P(x)=x\frac{1}{24}\left(A^4(x)+6A^2(x)A(x^2)+3A^2(x^2)+8A(x)A(x^3)+6A(x^4)\right) \]也即一个特殊标记的碳原子,四周连接烷基,总碳原子数为\(n\)的本质不同的情况数\(p_n\)满足的生成函数(证易)。
对于含有\(n\)个碳原子的本质不同的烷烃中碳碳单键等价类数的总和\(q_n\)也有类似的结论。被特殊标记的碳碳单键的地位等同于单烯烃中的碳碳双键,因此
\[ Q(x)=F(x)=\frac{(A(x)-1)^2+A(x^2)-1}{2} \]最后,我们将\(\eqref{5}\)式对于每个含有\(n\)个碳原子的本质不同的烷烃求和,就得到
\[ p_n-q_n+s_n=c_n \]而等式右端的\(c_n\)即为所求,它的生成函数是
\[ \begin{aligned} C(x)&=P(x)-Q(x)+A(x^2)-1\\ &=x\frac{1}{24}\left(A^4(x)+6A^2(x)A(x^2)+3A^2(x^2)+8A(x)A(x^3)+6A(x^4)\right)-\frac{(A(x)-1)^2-A(x^2)+1}{2} \end{aligned} \]- 烷烃计数 - Burnside引理

- 烷烃计数 - 立体异构
