2024 熵密杯 Write-ups



rank
doro_think

可能是因为赛题主要涉及的是密码算法的应用，所以感觉难度很低（相较于CTF中的各种奇形怪状的密码分析而言）。大致记录一下笔者写的几道题吧，在赛中没看的几道题后期也会补上去。


赛题分成两个部分，第一部分由三道Crypto基础题组成，任意完成一道即可进入第二部分，这三道赛题之间没有递进关系；第二部分有四道题，外加一个“最终目标”，完成最终目标之外的四道题才能获取到足够的信息来完成最终目标，第二部分的赛题有层层递进的关系，也有少部分是独立的。



附件在此：


将要加密的明文分成每16字节一组，加密过程为在GF(N)上将明文块乘上密钥，处理下一个块时，密钥自增一。本题中N是一个32字节的质数，因此解密过程就非常好办了，直接乘上密钥的逆元即可。

此外，题目中消息前有一个固定的前缀MSG_PREFIX，因此我们可以通过MSG_PREFIX[:16]与第一个密文块求出初始密钥。


Proof of Concept：


解出来是：

poLsYKw8ElIHB7jTtdjOmGQ0kvqlXnYI


附件在此：


自定义的块加密，主要流程为：

每一轮使用的轮密钥由derive_round_key生成，对于某一轮的轮密钥而言，它总是上一轮的轮密钥（或初始密钥）作为一个小端序无符号4字节整型加上1后的结果。

我们可以很轻松地写出解密函数decrypt，难点应该在四字节密钥的穷举（爆破）上（估计很多队在这一步上都消耗了大量时间）。明文开头四个字节是固定的pwd:，可以据此进行穷举，笔者尝试将密钥从00000000穷举到FFFFFFFF，同时从FFFFFFFF穷举到00000000来缩短时间，不过运气不错，用于加密的密钥开头为F8。对于一般的情况而言，在多台机器上多进程爆破应该可以将穷举时间缩短到原来的几十到几百分之一。


Proof of Concept：


解出来的加密口令是：

pwd:%@PRjd8)k5TV


附件在此：


第二个谜题要求通过协同签名的数据求解出服务器的私钥d2，先拿到一组数据：

r = 0x5371C63BA0E5DF688F3A9230CEE3E66E9042074A5938810C5922CB42AF0DDF0C
s2 = 0x583013D4C3080595942B514C100A55F49D2456C318ECE3FE311A3F2C2B53749E
s3 = 0x8CFC4953150A7320423CA99BA8BC961250AB3DF2A85B75434E305A43BBEE71FE

观察co-signing_server.c中的代码可知：

这里的\(n\)为SM2算法所使用的参数中椭圆曲线的阶。

p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0

显然我们有

\[ (s_3-s_2)r^{-1}\equiv d_2\pmod{n} \]

求出的d2为

d2 = 75133153874808200698750375741973887146735262423059242244009334005845482114914


附件在此：


本题要求以管理员的身份登录数据库管理系统。我们需要在登陆界面上填入用户的公钥文件，以及该用户的私钥文件来实现一个用户的登录，换句话说，我们需要伪造管理员shangmibeiadmin的私钥与证书来欺骗登录系统。

可以使用如下修改以后的gmssl工具来生成公私钥对：

// https://github.com/guanzhi/GmSSL/blob/master/src/sm2_key.c

// ...
    if (sm2_private_key_info_to_der(sm2_key, &p, &pkey_info_len) != 1
    || rand_bytes(salt, sizeof(salt)) != 1
    || rand_bytes(iv, sizeof(iv)) != 1
    || sm3_pbkdf2(pass, strlen(pass), salt, sizeof(salt), iter, sizeof(key), key) != 1) {
    error_print();
    goto end;
}

// Insert the code below in the corresponding place
    printf("SM2 private_key_der :\n");

    for(int i=0;i<SM2_PRIVATE_KEY_INFO_DER_SIZE;i++) printf("%02x",pkey_info[i]);

    BASE64_CTX ctx;
    uint8_t* b64 = NULL;
    int len;

    if (!pkey_info) {
        error_print();
        return -1;
    }

    // FIXME: use a fixed-size buffer
    if (!(b64 = malloc(SM2_PRIVATE_KEY_INFO_DER_SIZE * 2))) {
        error_print();
        return -1;
    }

    base64_encode_init(&ctx);
    base64_encode_update(&ctx, pkey_info, (int)SM2_PRIVATE_KEY_INFO_DER_SIZE, b64, &len);
    base64_encode_finish(&ctx, b64 + len, &len);

    printf("\n\n");

    printf("Private key:\n\x1b[34;1m");
    for(int i=36;i<36+32;i++) printf("%02x",pkey_info[i]);
    printf("\x1b[0m\n\n");
    printf("Public key:\n\x1b[34;1m");
    for(int i=86;i<86+64;i++) printf("%02x",pkey_info[i]);
    printf("\x1b[0m\n\n");
    
    printf("\x1b[33;1mNotice: You should manually copy the private key below or above.\x1b[0m");
    
    printf("\n\n\x1b[32;1m===== NOPASS START! =====\x1b[0m\n\n");
    printf("-----BEGIN EC PARAMETERS-----\n");
    printf("BggqgRzPVQGCLQ==\n");
    printf("-----END EC PARAMETERS-----\n");
    printf("-----BEGIN EC PRIVATE KEY-----\n");
    printf("%s", (char *)b64);
    printf("-----END EC PRIVATE KEY-----\n");
    
    printf("\n\x1b[32;1m=====  NOPASS END!  =====\x1b[0m\n\n\n");

    free(b64);

// End of modified code

    /*
    if (pkey_info_len != sizeof(pkey_info)) {
        error_print();
        goto end;
    }
    */
    sm4_set_encrypt_key(&sm4_key, key);

// ...

重新编译以后就可以通过gmssl sm2keygen -pass 114514来生成裸的公私钥对了：

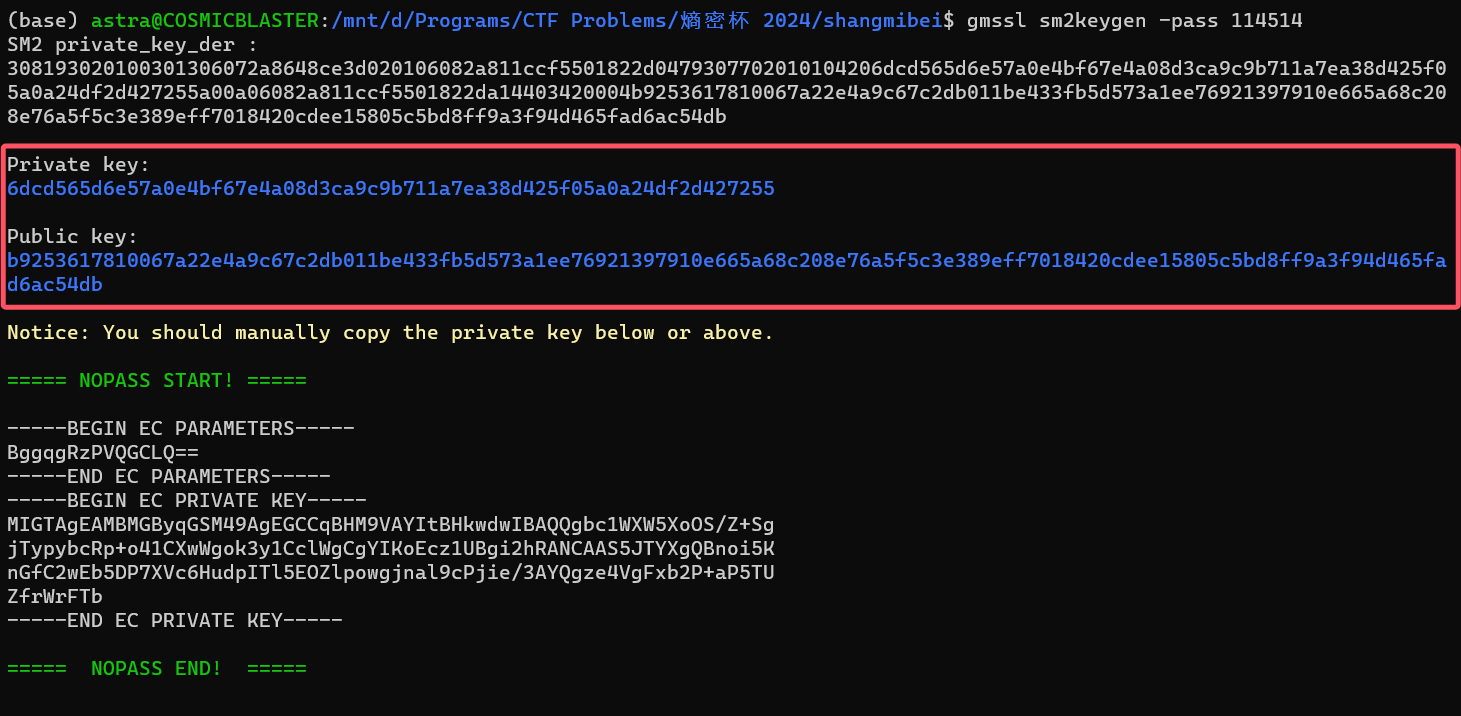
gmssl test

笔者首先尝试将证书中的128字节公钥替换为生成的公钥，并在登录界面中填入篡改后的证书文件与刚才生成的私钥，但是远端验证没有通过，原因大抵是还有一个签名没有也没办法直接篡改：（gmssl certparse < 数据库管理系统管理员证书.cer）

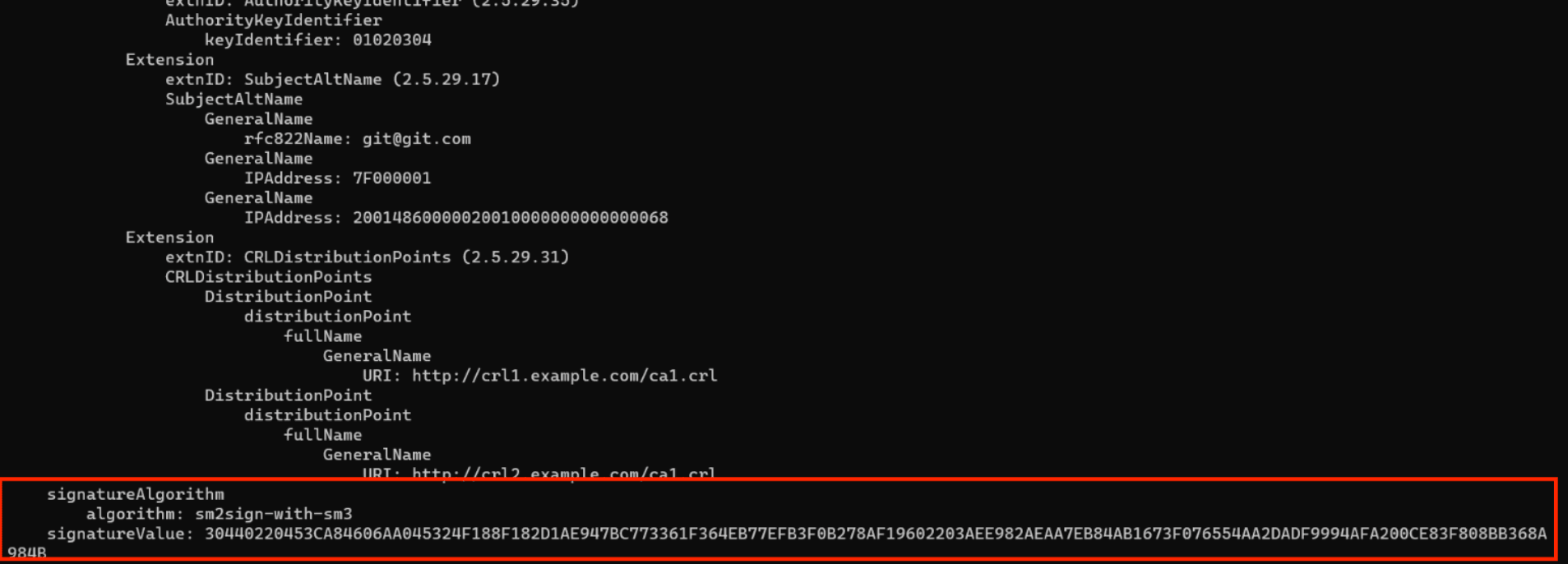
signature

然后笔者注意到登录界面上有一个注册的功能，里面可以自定义私钥与用户名，注册时系统会根据你提供的私钥与用户名自动创建一个证书文件。还是尝试生成一个私钥，然后以shangmibeiadm1N的名义注册，得到证书：

-----BEGIN CERTIFICATE-----
MIICXzCCAgWgAwIBAgIIYA+lRuKjwJQwCgYIKoEcz1UBg3UwNjELMAkGA1UEBhMC
Q04xEzARBgNVBAoTClNoYW5nTWlCZWkxEjAQBgNVBAMTCVNoYW5nTWlDQTAeFw0y
NDA5MDQwODA3NDdaFw0yNTEwMTAxMjAxMDFaMFUxEzARBgNVBAoTClNoYW5nTWlC
ZWkxFzAVBgNVBAsTDlNoYW5nTWlCZWkyMDI0MRgwFgYDVQQDEw9zaGFuZ21pYmVp
YWRtMU4xCzAJBgNVBAYTAkNOMFkwEwYHKoZIzj0CAQYIKoEcz1UBgi0DQgAEYbu/
UWIdr/GX1HOX17jB/hcXfI90ZW+9+YNnoEg7jbF8ZipLYjirpQNF0hLzJY7e7SdQ
E6IHOZnsb2s70XM8WaOB3TCB2jAOBgNVHQ8BAf8EBAMCA4gwHQYDVR0lBBYwFAYI
KwYBBQUHAwIGCCsGAQUFBwMBMA8GA1UdDgQIBAYBAgMEBQYwDwYDVR0jBAgwBoAE
AQIDBDAuBgNVHREEJzAlgQtnaXRAZ2l0LmNvbYcEfwAAAYcQIAFIYAAAIAEAAAAA
AAAAaDBXBgNVHR8EUDBOMCWgI6Ahhh9odHRwOi8vY3JsMS5leGFtcGxlLmNvbS9j
YTEuY3JsMCWgI6Ahhh9odHRwOi8vY3JsMi5leGFtcGxlLmNvbS9jYTEuY3JsMAoG
CCqBHM9VAYN1A0gAMEUCIC0CGXYG9bAlV2vPYbz7+KcGYafELfwrJikA5Idfu6PK
AiEAoRDx/zVEbha5L2JTAGMI3V3rpFoiP7kBHWxuGLQLZJg=
-----END CERTIFICATE-----

可以看到用户名：

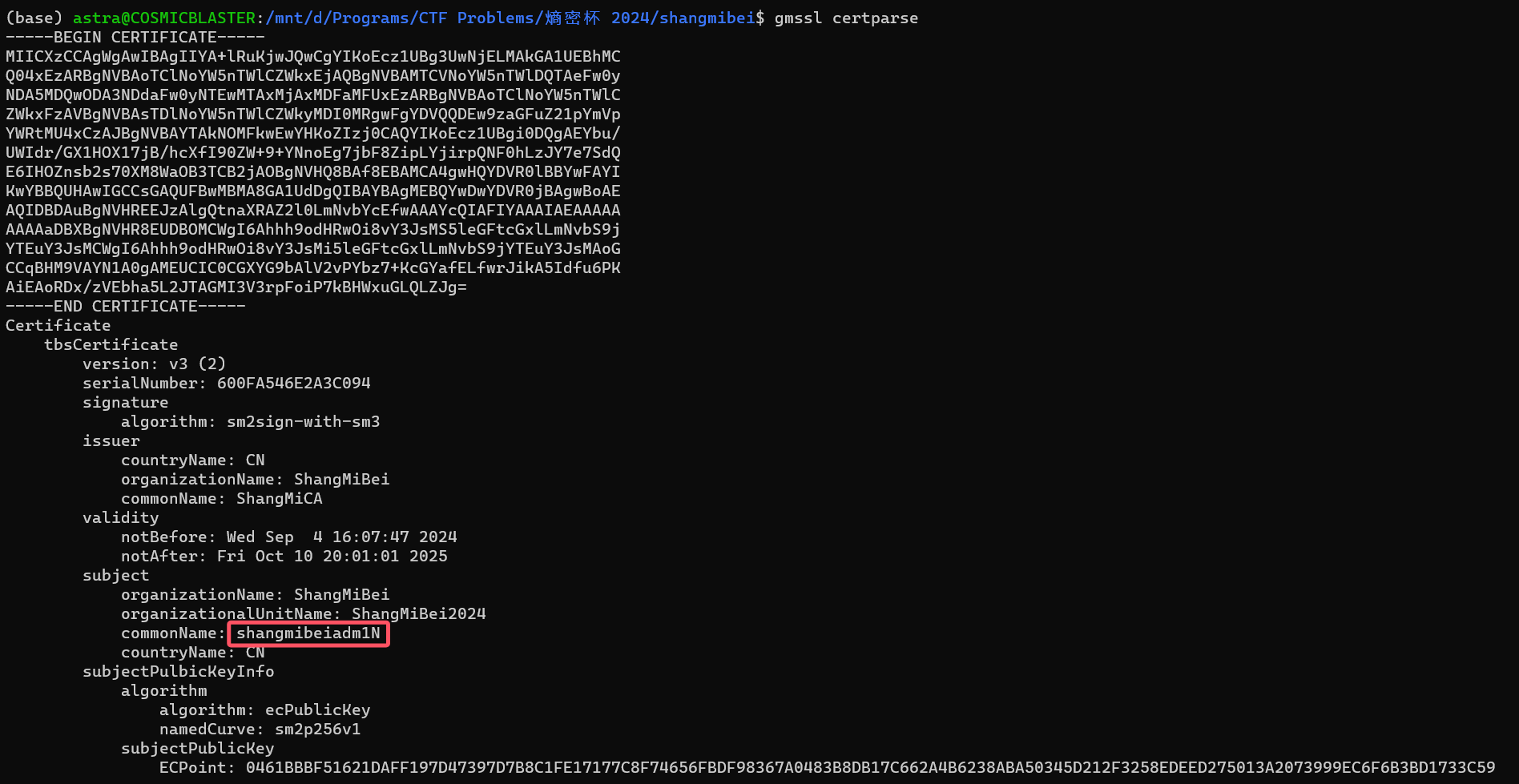
fake username

将上述base64数据解码后把shangmibeiadm1N替换为管理员的名称shangmibeiadmin，重新base64编码后和刚才生成的私钥一起发送给远端，即可欺骗登陆系统，以管理员的身份登录。



附件在此：


第二部分的第四关是一个经典的漏洞——被截断的线性同余生成器（Linear Congruential Generator，LCG）用来生成的随机数是可以预测的。Minecraft的1.8~1.12.2版本中就使用了这种随机数生成器（Java），在共用种子的情况下，玩家可以通过一个生成器产生的随机数（如物品掉落位置）来预测或者反推另一个生成器产生的随机数（参考Randar漏洞：https://github.com/spawnmason/randar-explanation）。预测这种LCG的手段是密码分析中的一个有力工具：格基约化（Lattice Reduction）（奇怪的是，主办方在参赛手册中并未提醒参赛选手事先准备好诸如fplll、SageMath之类支持格基约化的工具）。

本题在IV的生成过程中使用了三次这种LCG，之所以说是三次是因为每次种子的迭代过程都可以化简为：

\[ \newcommand{\mul}{\text{MULTIPLIER}} \newcommand{\add}{\text{ADDEND}} \begin{aligned} s_{i+1} &\equiv \underbrace{\mul\cdot (\mul\cdot (\cdots(\mul}_{1000}\cdot s_i + \underbrace{\add) + \cdots) + \add) + \add}_{1000}\\ &\equiv as_i + b \pmod{N} \end{aligned} \]

其中

\[ N=\text{MASK}+1=2^{64} \]

笔者在此给出两种恢复种子的方式。首先可以尝试构造如下的格基：

\[ A= \begin{pmatrix} \alpha\cdot a & & & 1 & & & &\\ -\alpha & \alpha\cdot a & & & 1 & & &\\ & -\alpha & \alpha\cdot a & & & 1 & &\\ & & -\alpha & & & & 1 &\\ \alpha\cdot (a\tilde{x}_0+b-a\tilde{x}_1) & \alpha\cdot (a\tilde{x}_1+b-a\tilde{x}_2) & \alpha\cdot (a\tilde{x}_2+b-a\tilde{x}_3) & & & & & \beta\\ \alpha\cdot N & & & & & & &\\ & \alpha\cdot N & & & & & &\\ & & \alpha\cdot N & & & & &\\ \end{pmatrix} \]

其中

\[ \tilde{x}_i=s_i-x_i \]

是种子\(s_i\)的高32比特位，\(x_i\)未知。而\(\alpha\)与\(\beta\)都是大整数，\(\beta\)的作用是确保能够规约出一个格点，它在第五个基向量上的坐标分量为\(\pm 1\)，而\(\alpha\)的作用是确能够规约出一个格点，它的前三个分量都是\(0\)。将上述格基规约以后可以找到一个格点：

\[ (0,0,0,x_0,x_1,x_2,x_3,\beta) \]

据此我们恢复出了四个迭代过程中的种子\(s_0,s_1,s_2,s_3\)。


第二种方法基于最近向量问题（Closest Vector Problem，CVP），并且显得更为简洁。考虑如下的格基：

\[ B= \begin{pmatrix} 1 & a & a^2 & a^3\\ & N & & \\ & & N & \\ & & & N \\ \end{pmatrix} \]

\(B\)中含有如下的格点：

\[ (x_0+\tilde{x}_0, x_1+\tilde{x}_1-b, x_2+\tilde{x}_2-ab-b, x_3+\tilde{x}_3-a^b-ab-b) = (s_0, s_1, s_2, s_3)\cdot B \]

我们知道

\[ 0 \le x_i < 2^{32} \]

因此我们可以在

\[ \boldsymbol v = (c+\tilde{x}_0, c+\tilde{x}_1-b, c+\tilde{x}_2-ab-b, c+\tilde{x}_3-a^2b-ab-b) \]

的附近寻找\(B\)中的格点，找到的格点很有可能就是我们所需要求的。上式中

\[ c = \frac{2^{32}}{2} \]

无论采用哪一种方式，求出了生成IV使用的种子后，我们也能预测出密钥的值，之后使用GmSSL-Python中的SM4分组密码解密密文即可。


Proof of Concept：



附件在此：


第二部分中的所有题目其实都是互通的，第二关中解出的服务器私钥也可以用在我们的最终目标中。与第二关类似，观察co-signing_client.js中的代码，我们知道：

稍作化简即可消去\(k\)，最终整理得到：

\[ d_1\equiv (s+r-s_1^{-1}s_2r_1)\cdot (s_1^{-1}s_2e+s_3)^{-1} \pmod{n} \]

现在，上述等式右端的变量值全部都是已知的（数据取自总经理的协同签名），因此我们能够计算出总经理端的私钥\(d_1\)，然后我们还知道服务端的私钥\(d_2\)，据此我们终于可以以总经理的身份伪造签名了。

d1 = 90919127323695568397119051689582862352296983775157729258730148362152821090405
d2 = 75133153874808200698750375741973887146735262423059242244009334005845482114914
r  = 28730176605439163472921640563553053292653891145888922558062915403116989836605
s  = 86242668082472195916100635815716613522346819350645381713830905067386456446833
    
k1 = 114514
k2 = k3 = 1919810

完结撒花🥳🥳🥳🍾🍾🍾🎉🎉🎉🎊🎊🎊

finale



现在回过头来看看第一部分没整的两道题。

附件在此：


看上去是SM3长度扩展攻击。嗯……看不出题目具体长啥样，只能先这么猜测了。这类攻击的脚本在GitHub上能找到许多。

不过这告诉我们打熵密杯之前一定要把各种SM相关的代码能准备多少就准备多少（多玩SM），方便打板子😈😈😈。


附件在此：


看上去是一个LWE（Learning With Errors）问题，但是完全没有想象中的那么复杂，并且由于题目中使用的矩阵是一个GF(q)上的满秩方阵\(A\)，尝试求解最近或者最短向量理论上其实是不可行的，因为\(A\cdot s\)可以取到任何向量的值。

再次观察代码，可以发现加密过程中使用的误差向量规模非常的小，样本空间大小为\(2^{16}\)，更重要的是，我们可以通过尝试求解加密过程中的m向量，并观察m的每个分量是否都是0或1来判断所求的m是否正确。因此我们至多只需要穷举\(2^{16}=65536\)次即可恢复出明文。


Proof of Concept：



















Tags: #熵密杯, #Cryptography, #LatticeBasedCryptography, #LinearCongruentialGenerator

Time: 2024-09-09 16:34